Ortak Merkezli Küreler Kuramı

Yunan filozofları, gezegenlerin hareketlerini rasyonel bir şekilde açıklamaya çalışarak astrolojinin ötesine geçen yeni bir yaklaşım başlattılar. Küresel ve dairesel hareket, göksel hareket için tercih ettikleri idealdi ve iki bin yıl boyunca bu şekilde kaldı. Geometrik formlar olarak küre ve daire Yunan matematiğinde çokça araştırıldı. Ayrıca her zaman orijinal noktasına geri dönen mükemmel dairesel hareket, ilahi varlıklar veya en azından ebediyen var olan nesneler olarak kabul edilen gök cisimleri için uygun görünüyordu. Dünyadan bakıldığında gök küresi mükemmel, tekdüze bir şekilde dönüyor gibi görünüyordu.

Platon öğrencilerine gezegenlerin karmaşık hareketlerini nasıl açıklayabileceklerini sordu. Öğrencilerinden Knidos’lu Eudoxus (yaklaşık M.Ö. 408-355) bu mücadeleyi üstlendi. Eudoxus’un diğer başarıları arasında, modern integral hesabına benzer şekilde, alan ve hacim formülleri türetme yöntemi de bulunmaktaydı.

Knidos’lu Eudoxus’un (Knidos’un kalıntıları bugünkü Datça’da bulunur) Dünya etrafında dönen gökcisimlerinden oluşan ortak merkezli küreler teorisi, kafa karıştırıcı geri giden döngüler de dâhil olmak üzere gökyüzünün hareketlerini bazı ayrıntılarıyla açıklayan ilk matematiksel modeldi. Model, kendi eksenleri etrafında farklı yollarda fakat aynı hızlarda dönen kürelere dayanıyordu. Bu eksenler bir iç küreyi diğerine bağlıyordu ve birbirlerine sabit açılarla eğimliydiler. Tüm gezegenlerin ötesinde, hareketsiz Dünya’nın etrafında günde bir kez aynı şekilde dönen sabit yıldızlardan oluşan bir gök küresi vardı.

Dünya’dan bakıldığında gezegenin yolu her gezegene kendine özgü hareketler sağlayan, birbirine bağlı kürelerden oluşan bir daireden daha karmaşıktı. Daha düzgün hareket eden Güneş ve Ay üçer hareketle dönüyorlardı. Birincisi, günlük hareketi oluşturmak için kuzey-güney ekseninde dönen bir Güneş ve Ay inancıydı. İkincisi, ekliptiğin gök ekvatoruna göre eğimini içerecek şekilde birinciye göre eğikti ve her gökcismi, kendi periyodunda bir kez dönüyordu. Ay bunu 28 günde, Güneş ise 365 günde tamamlıyordu. Son olarak üçüncüsü, gökcisimlerinin Dünya’ya uzaklıklarının döngü içerisinde değişimlerini açıklıyordu. Bu da onların ekliptikten sapmalarını içerecek şekilde eğimli bir yol ile döndüğü sonucuna götürüyordu.

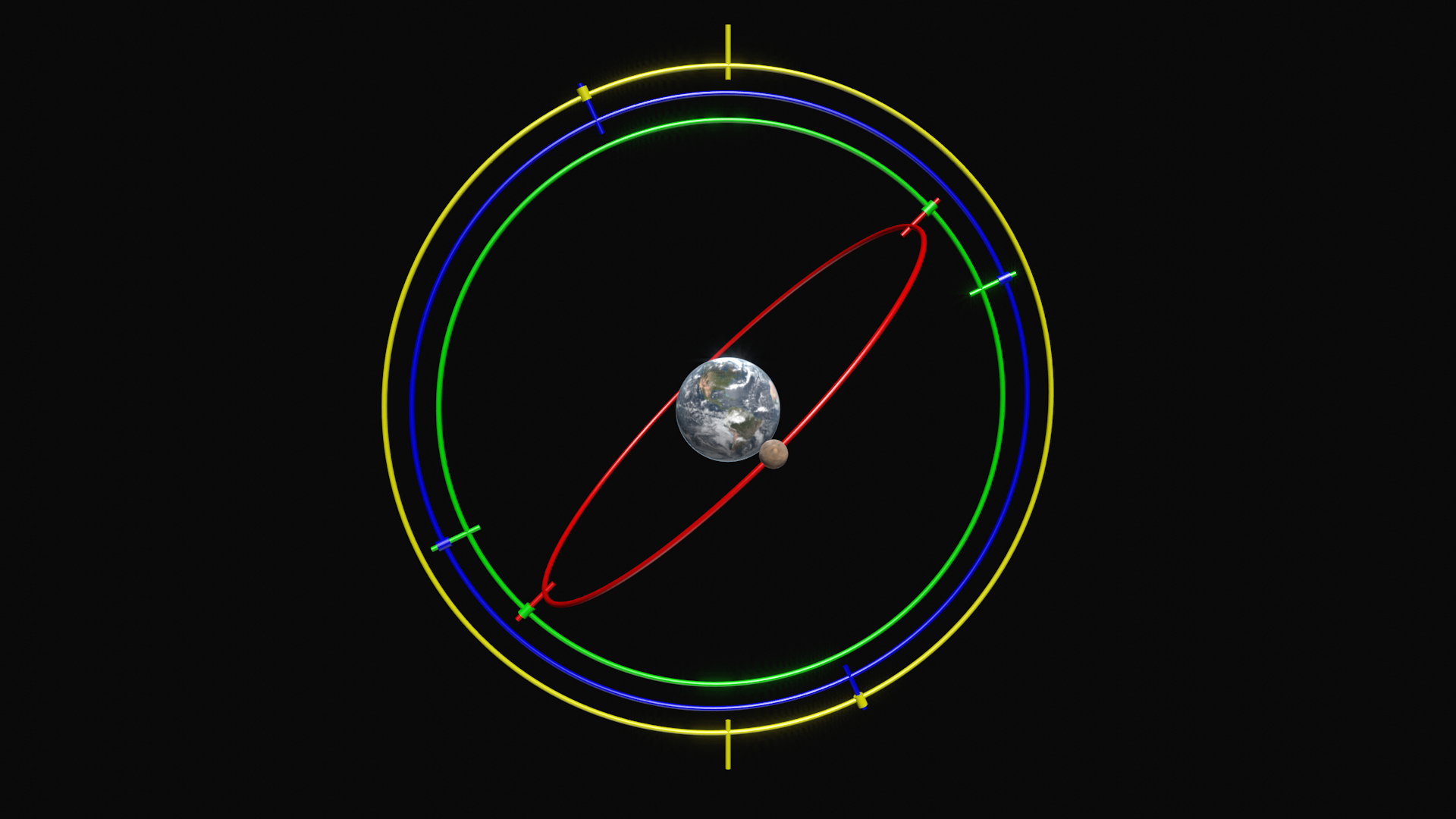
Eudoxus, oluşturduğu modelle o dönemde bilinen gezegen hareketlerini oldukça iyi açıklayabiliyordu. Ancak Mars’ın hareketlerinin, modelle eşleşmesi neredeyse imkânsız olan zorlu bir durum oluşturduğu ortaya çıktı. Eudoxus, buna cevap olarak modelin gerçek bir fiziksel yapıyı temsil etmediğini, ortak merkezli olarak iç içe geçmiş olsalar bile bir gezegenin küre kümesinin diğerinin hareketini etkilemediği, tamamen matematiksel bir yapı olduğunu söyledi.

Knidoslu Eudoxus, Platon ile Pisagor’un kozmolojik spekülasyonlarından etkilenmişti. Gezegenlerin algılanan tutarsız hareketlerini açıklamak ve gök cisimlerinin hareketini doğru bir şekilde hesaplamak için tek tip bir model geliştirmek amacıyla ortak merkezli küreler fikrini ortaya attı. Kitaplarından hiçbiri günümüze ulaşamamıştır ve kozmolojik teorileri hakkında bildiğimiz her şey Aristoteles ve Simplicius’un çalışmalarından gelmektedir. Bu çalışmalara göre Eudoxus’un modeli yirmi yedi ortak merkezli küreye sahipti ve her küre, her gök cismi için gözlemlenebilir bir hareket tipini açıklıyordu. Eudoxus, sabit yıldızlara, onların günlük hareketlerini açıklayacağı varsayılan bir küre tahsis etmişti.

Eudoxus’un çağdaşı olan Callippus, ortak merkezli kürelerin toplam sayısını artırarak sistemini geliştirmeye çalıştı. Güneş ve Ay için iki kürenin yanı sıra Mars, Merkür ve Venüs için de bir ek küre ekledi. Bu ek kürelerin Eudoxus’un orijinal sistemindeki bazı hesaplama problemlerini çözmesi gerekiyordu. Callippus’un sistemi belirli gök cisimlerinin hareketlerini daha iyi tahmin edebiliyordu ancak sistemi hala birçok sorunla karşı karşıyaydı ve birçok astronomik gözlemi açıklayamıyordu.

Aristoteles, Metafizik ve De Caelo’da (Gökler) kendi ortak merkezli küreler sistemini geliştirdi. Hem Eudoxus’un hem de Callippus’un modellerinde çok az küre bulunduğunu düşündü ve Callippus’un sistemine daha fazla küre ekledi. Aristoteles’in gezegen modeli, Dünya merkezli toplam 56 küreyi kullanmasıyla Eudoxus’un modelinin genişletilmiş bir versiyonunu oluşturuyordu. Aristoteles küreleri fiziksel varlıklar (bir çeşit göksel kristal) olarak görmüştü. Ancak evrenin armoni gösteren sayılarla düzenlendiği fikri üzerine kurulu bir varsayım olan Pisagor’un kürelerin müziği hakkındaki fikrini reddetti. Tam tersine, göklerin sessizliğini küre taşıyıcılarının bir kanıtı olarak görüyordu; eğer gök cisimleri bir ortamdan hızla geçselerdi gürültü beklenirdi. Kürelerin sayısı daha fazlaydı çünkü Aristoteles, sabit yıldızların dış küresinin temel günlük hareketinin yukarıdan aşağıya aktarılmasını sağlayacak şekilde her gezegene ait küre takımlarını ek kürelerle birbirine bağlamak istiyordu.

Yer merkezli model olarak da bilinen ortak merkezli küre astronomisi, 16. yüzyılda güneş merkezli model tarafından yıkılmadan önce yüzyıllar boyunca kozmosu açıklamanın hâkim görüşü oldu. Ortak merkezli küreler kuramı; görünen hareketi açıklanması, gökbilimcilerinin tutulmalar ve kavuşumlar gibi çeşitli gök olaylarını göreceli doğrulukla tahmin edip hesaplayabilmesi açısından önemliydi. Kozmolojik bir çerçeve çizerek evrende gözlemlenen düzen ve yapının açıklanmasına yardımcı olmasıyla da zamanının başarılı bir astronomik gelişmesiydi.